Быстрое вейвлет-преобразование в пространстве сплайновых вейвлетов на конечном отрезке
Область применения - анализ данных, численные методы.
Вейвлет-системы дают ряд преимуществ для широкого круга задач перед классическими ортогональными системами функций благодаря своим аппроксимационным свойствам и локализации во временной и частотной областях. Вейвлеты чрезвычайно перспективны для применения в задачах обработки сигналов, распознавания образов, сжатия информации.
Программа позволяет построить прямое и обратное вейвлет-преобразование на базе полиномиальных сплайнов. В программе реализованы следующие возможности:
- построение вейвлет-базисов в пространстве полиномиальных сплайнов;
- получение графиков и матрицы значений центральных и граничных вейвлет-функций;
- получение коэффициентов вейвлет-преобразования по набору входных данных и обратно;
- определение начальных параметров преобразования - отрезка и степни спалйна;
- сохранение полученных данных в виде отчета;
Алгоритм реализован для полиномиальных сплайнов степени m={2,3,4}.
Объем входных-выходных данных для обратного вейвлет-преобразования:
| Степень сплайна | Кол-во входных параметров - коэффициентов преобразования | Кол-во выходных параметров - значений функции на сетке |
| 2 | 9 | 8 |
| 3 | 18 | 16 |
| 4 | 35 | 32 |
Входным параметром для прямого вейвлет-преобразования является функция, выходными данными является набор коэффициентов преобразования (соответствует второму столбцу таблицы).
В приложениях важно уметь решать две следующие задачи:
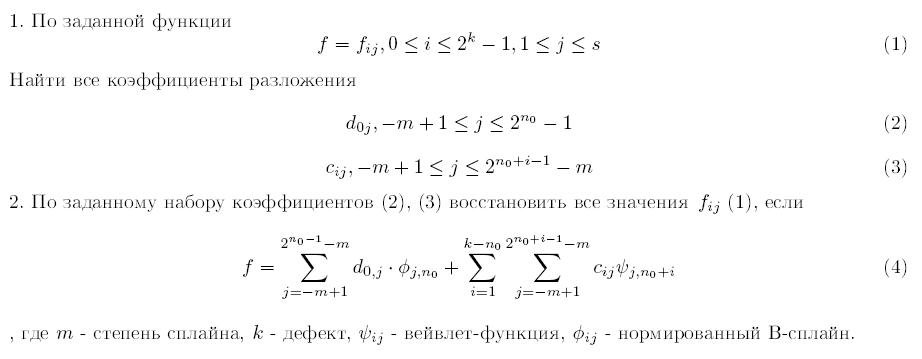
Решение первой задачи называется прямым вейвлет-преобразованием, решение второй задачи - обратным вейвлет-преобразованием. Поскольку носители построенных вейвлет-функций содержат конечное, не зависящее от дефекта, число частичных отрезков, то они очень хорошо локализованы во временной области. Т.к. они являются линейными комбинациями фиксированного числа B-сплайнов, то они хорошо локализованы и в частотной области. Поэтому коэффициенты разложения по ним непериодического сигнала несут как информацию о его поведении на коротком отрезке времени, так и о его "мгновенном спектре".
Используемые материалы - работы заведующего кафедры Высшей математики Поволжского государстенного университета телекоммуникаций и информатики д.ф.-м.н. Блатова Игоря Анатольевича, в частности алгоритм вейвлет-преобразования на основе полиномиальных сплайнов, используемый в основе программы.
Инструментальные средства создания - C++ Builder 6.
Во вложении два главных файла:
- FWTSplain.pdf - описание программы;
- FWTSplain.zip - архив с исходным кодом программы.
Литература:
- Блатов И.А. Полуортогональные сплайновые вейвлеты и метод Галеркина численного моделирования тонкопроволочных антенн / И.А.Блатов, Н.В.Рогова // Журнал вычислительной математики и математической физики. Самара, том 53, №5 : 2013. 727-736 с.
- Блатов И.А. Псевдоразреженные матрицы и прикладной вейвлет-анализ, Сборник научных трудов sworld по материалам международной научно-практической конференции, 2012, 84–86 с.
ОС - Windows XP и выше;
Свободная память 20 Mb;
RAM 30 Mb.
| Вложение | Размер |
|---|---|
| fwtsplain.zip | 1.08 МБ |
| fwtsplain_formuls.jpg | 31.95 КБ |
| fwtsplain.pdf | 397.4 КБ |
